Introduction
BTree is the index type used by default on CREATE INDEX. As I said in the introduction to indexes article, BTrees are also created automatically for primary key and unique constraints.
Before I start going into the internal structure of BTree, I’d like to talk to you about pageinspect_inspector, a python library to generate a graphical representation of what’s going on inside PostgreSQL’s BTrees. You pass your index to it on a command line and it generates an HTML allowing you to explore pages and items of your index. I wrote it using the extension pageinspect. All the images in this article come from it.
Here is a little video to show you how it works (where you might notice that I’m not a great frontend developer).
What is a BTree ?
BTree stands for balanced tree. In a balanced tree, all the leaves are at equal distance from the root. Moreover the root and parents can have more than two children which minimize the depth of the tree.
Here is a comparison of the same data in the form of a binary tree and a balanced tree.
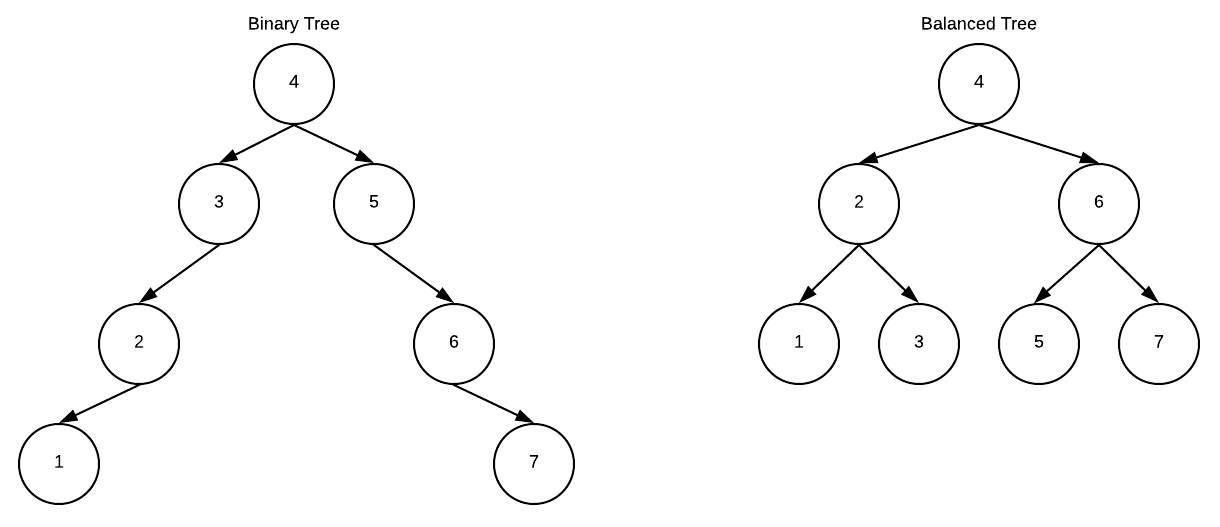
BTrees in postgres
Postgres implements the Lehman & Yao Btree which has a few specificities that you will discover in this article, or if you’re really into it, go read their research paper. I did and it was a lot of fun (I guess).
Let’s talk again about crocos. So as we said in the previous article, crocodiles eat candies like a 10yo left alone with money for dinner, and their number of teeth changes over life. It grows and then when they get old, they fall. Like humans. (Honestly, this is probably not 100% accurate, if you’re a vet, sorry about that, also, what are you doing here?). So, we want to be able to filter on the number of teeth and run queries like:
SELECT email FROM crocodile WHERE number_of_teeth < 18;
For that, we decided to create the following index.
CREATE INDEX ON crocodile (number_of_teeth);
Metapage
I generated the html for this index using pageinspect_inspector and here a first screenshot.
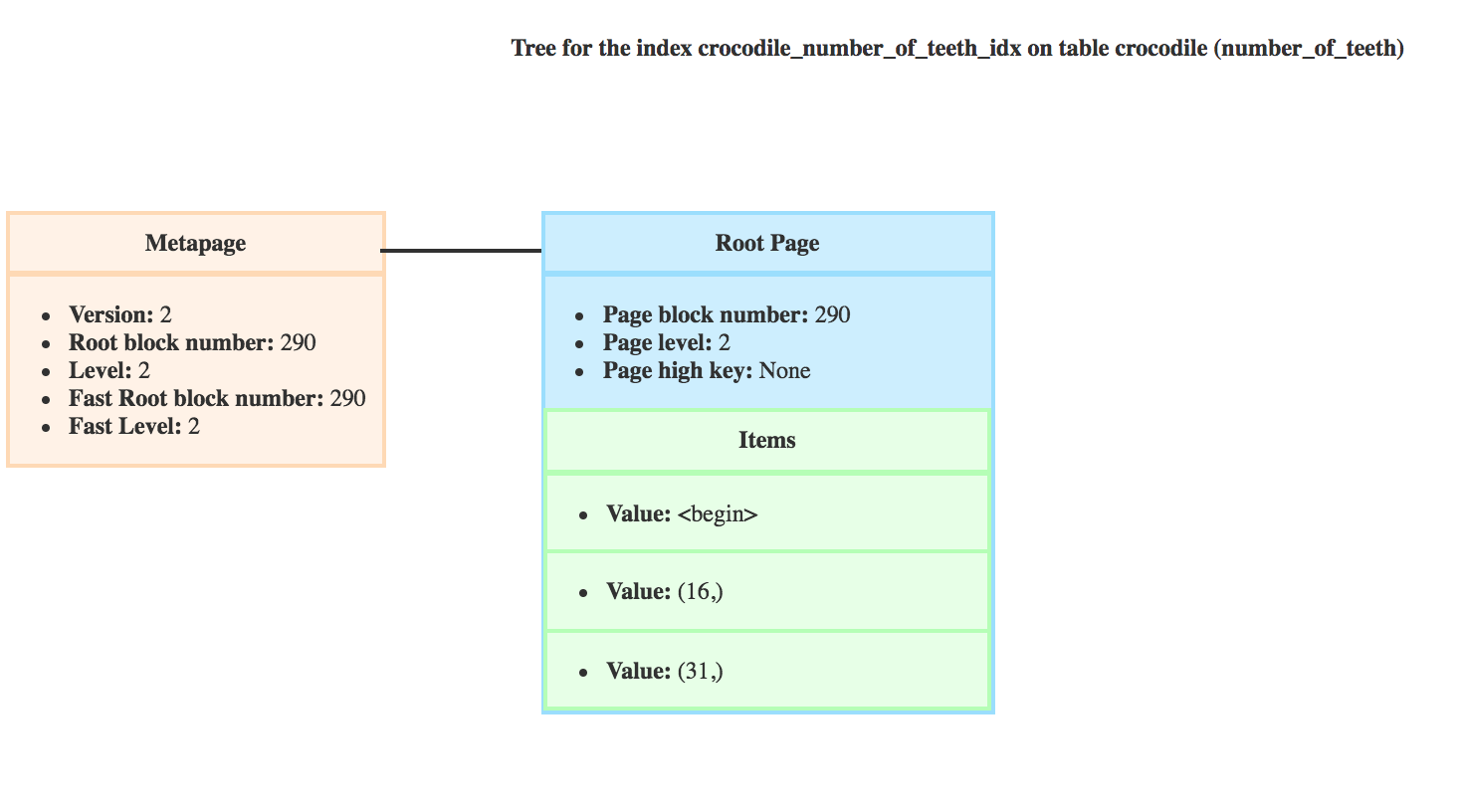
Here we see the metapage of the index and the root. The metapage is always the first page of a posgres index. It contains:
- The block number of the root
- The level of the root
- A block number for the fast root
- The level of the fast root
The pointer to the root can change. It’s a bit early to go into the details, but after an insert, it can be necessary to split the current root into two pages, in which case a new root is created with pointers on the split pages. Page splits will be detailed in the insert algorithm part of the next article.
If you prefer using pageinspect here is the query returning information on the metapage.
croco=# SELECT * FROM bt_metap('crocodile_number_of_teeth_idx');
magic | version | root | level | fastroot | fastlevel
--------+---------+------+-------+----------+-----------
340322 | 2 | 290 | 2 | 290 | 2
(1 row)
You may be confused by this fast root thing that here is redundant with the root, but let’s keep some of the suspense for the deletion algorithm part…
Pages and items
Pages
The root, the parents, and the leaves are all pages with the same structure. Pages have:
- A block number, here the root block number is 290
- A pointer to the next and previous pages
- A high key
- Items
Next and previous pages pointers
Thanks to the pointers to next and previous pages, pages in the same level are a linked list. This is a specificity of the Yao and Lehmann BTree. For example it’s very usefull in the leaves for ORDER BY queries.
Here would be the pages on the level 0 (leaves)
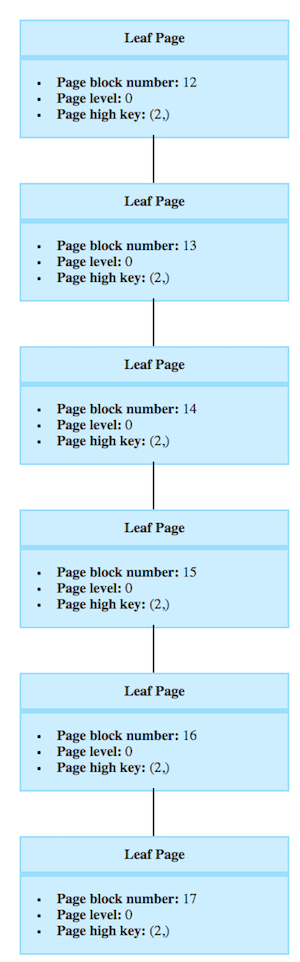
If we wanted to run the query
SELECT email FROM crocodile ORDER BY number_of_teeth ASC
Postgres would start at the first leaf page and thanks to the next page pointer, has directly all rows in the right order.
About the high key
The high key is also specific to Lehman & Yao BTrees. Any item in the page will have a value lower or equal to the high key.
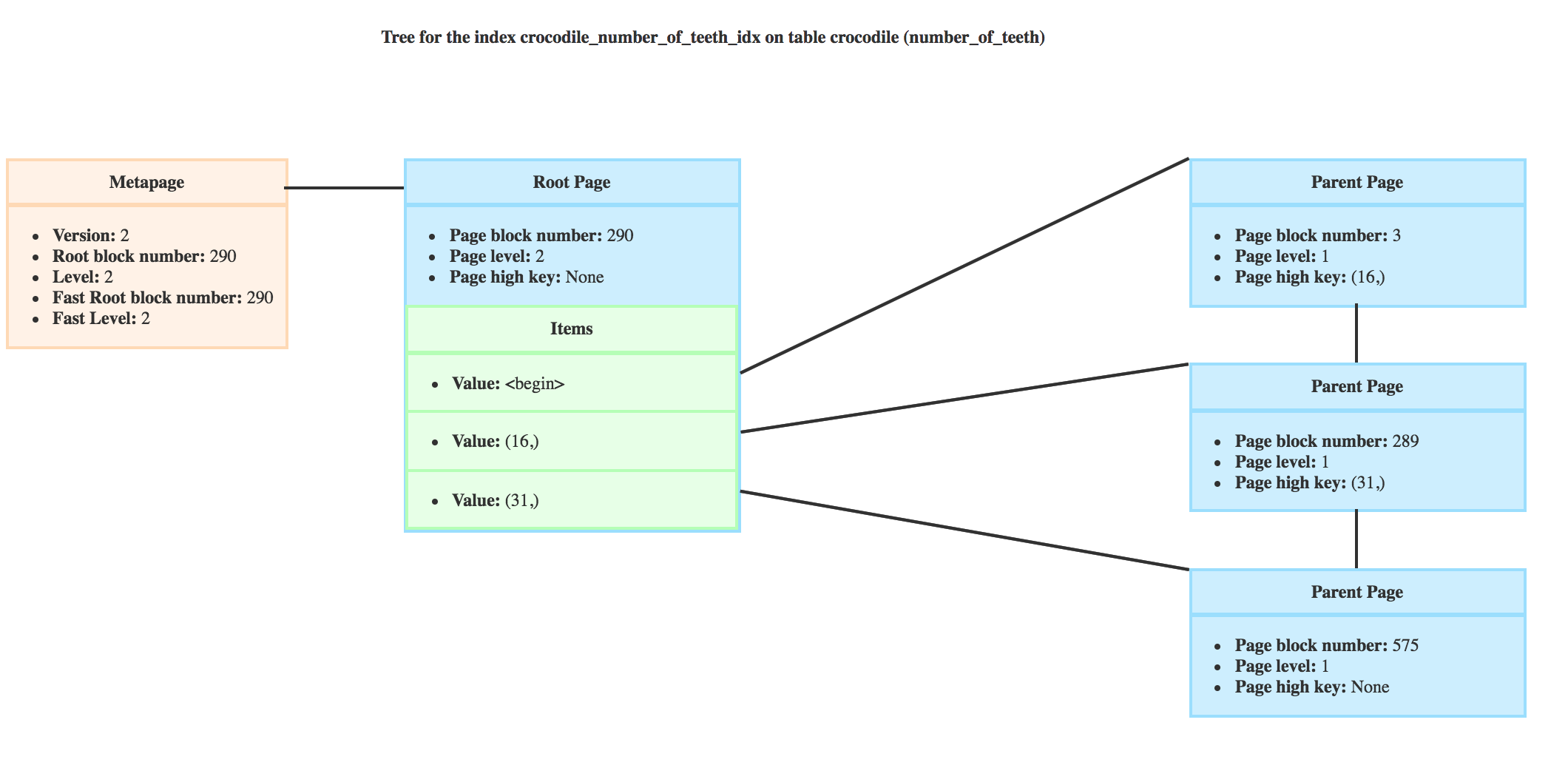
The root doesn’t have a high key, but for example in a parent level of my crocodile’s teeth index, like this one
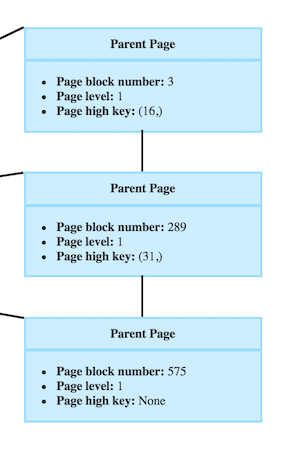
I can see that in the page 3, I will find crocodiles with 3 or less teeth, in page 289, with 31 and less, and in page 575, there is no high key as it’s the rightmost page.
pageinspect allows you to have more information on BTree pages
croco_test=# SELECT * FROM bt_page_stats('crocodile_number_of_teeth_idx', 289);
-[ RECORD 1 ]-+-----
blkno | 289
type | i
live_items | 285
dead_items | 0
avg_item_size | 15
page_size | 8192
free_size | 2456
btpo_prev | 3
btpo_next | 575
btpo | 1
btpo_flags | 0
Items
The items of a page (that are in green in my drawings) have a value and a ctid. The ctid indicated the physical location of a heap tuple, you can read about it in the previous article.

If you use the pageinspect extension, you will see that the first item of a page defines the high key like following:
croco_test=# SELECT * FROM bt_page_items('crocodile_number_of_teeth_idx', 12);
-[ RECORD 1 ]-----------------------
itemoffset | 1
ctid | (163,87)
itemlen | 16
nulls | f
vars | f
data | 02 00 00 00 00 00 00 00
-[ RECORD 2 ]-----------------------
itemoffset | 2
ctid | (49,46)
itemlen | 16
nulls | f
vars | f
data | 02 00 00 00 00 00 00 00
-[ RECORD 3 ]-----------------------
itemoffset | 3
ctid | (49,52)
itemlen | 16
nulls | f
vars | f
data | 02 00 00 00 00 00 00 00
The difference between the parents/root level and leaves is that the ctid of a parent level page would point to a child page. In the leaves, the ctid is the one from the row.
The value of an item in a leaf page is the value of the column(s) of the row. The value of an item in a parent page is the value of the first item in the child page.
Here is what leaf level items look like.

To sum it up
- A Btree is a balanced tree. PostgreSQL implements the Lehmann & Yao algorithm.
- A BTree starts with a metapage containing information on the root and fast root block numbers and levels.
- Root, parent, and leaves are pages. Each level is a linked list making it easier to move from one page to an other within the same level.
- Pages have a high key defining the biggest value that can be found and inserted in the page.
- A page has items. In the root or the parent levels, the items point to a page on the child level. In the leaves, it points to the heap of the row in the table.
Sometimes an image is worth a thousand words, so don’t hesitate to try pageinspect_inspector to visualize one of your own BTree indexes.
In the next article we will go over the algorithms used to search and maintain a BTree index.